Análisis de datos con Calc

Ahora que se han dado muchos reflectores al análisis de datos (pues su importancia en la era de la información es evidente), hay muchas personas que buscan cómo usar las herramientas de que disponen para llevar a cabo estas tareas, sino de una manera masiva con miles de miles de datos y registros, sí para las aplicaciones de pequeños negocios, de colectivos de incidencia pública, de investigación sociológica, médica o de cualquier otra disciplina científica, etc. que tengan “pocos” datos y que el análisis no se tenga que repetir muchas veces.

Pues LibreOffice Calc no se queda atrás en relación con otras suites de oficina. Y aquí vamos a describir cómo hacer muchos tipos de análisis de datos con nuestra herramienta favorita.

Lo primero es reconocer dónde están estas herramientas de estadística y manejo de datos dentro del programa. Sí, ya sé que a casi nadie le gusta leer los manuales ni las guías (y miren que las traducimos con mucho amor y cuidado). Es en el capítulo 9 «Análisis de datos» de la Guía de Calc, donde mejor se describen estas herramientas  y se indica cómo se deben usar (con ejemplos) e instructivos sencillos. En fin…

Para poner mi granito de arena, voy a tratar de acortar el árido (para algunos) pasaje y vamos a revisar el menú Datos. Tenemos varias herramientas a la vista para trabajar con un intervalo de celdas: ordenar, filtrar, categorizar, graficar, resumir, consolidar y aplicar ciertos métodos de estadística. No es poco, en verdad. Confío en que cualquiera puede explorar el menú Datos a su antojo.

Por ahora y para este pequeño artículo nos vamos a concentrar en el primer paso de cualquier proyecto de tratamiento de datos: la estadística descriptiva. Yo he tomado algunos archivos de ejemplo que ya existen y son compartidos de manera pública, pero tú vas a utilizar los datos de tu proyecto.

Un sitio estupendo para practicar, aprender y divertirse con las hojas de cálculo y la estadística:
HojaMat.es ::: Aprender y divertirse con la hoja de cálculo.

Algunos sitios web con fuentes de datos para prácticas y ejemplos:

• https://filesamples.com/formats/csv
• https://data.world

Análisis descriptivo de los datos

1. Histogramas y tablas de frecuencias

Un histograma es una representación gráfica de una tabla de frecuencias. Y esta, a su vez, es la clasificación de los valores de una variable para comprender mejor cómo se distribuyen estos en la población que los componen. Dicho esto, puedes leer la explicación en Wikipedia para quedar más claros: https://es.wikipedia.org/wiki/Histograma.

Ahora bien, emplear un menú o una función para crear un histograma en Calc a partir de tus datos aún no es posible. Lo siento. Sin embargo, sí se puede generar una tabla de frecuencias y de ahí generar el histograma deseado. Es un pelín más latoso, pero es perfectamente posible. Voy a poner un ejemplo para una variable que registra las diferentes alturas de unos alumnos de secundaria.

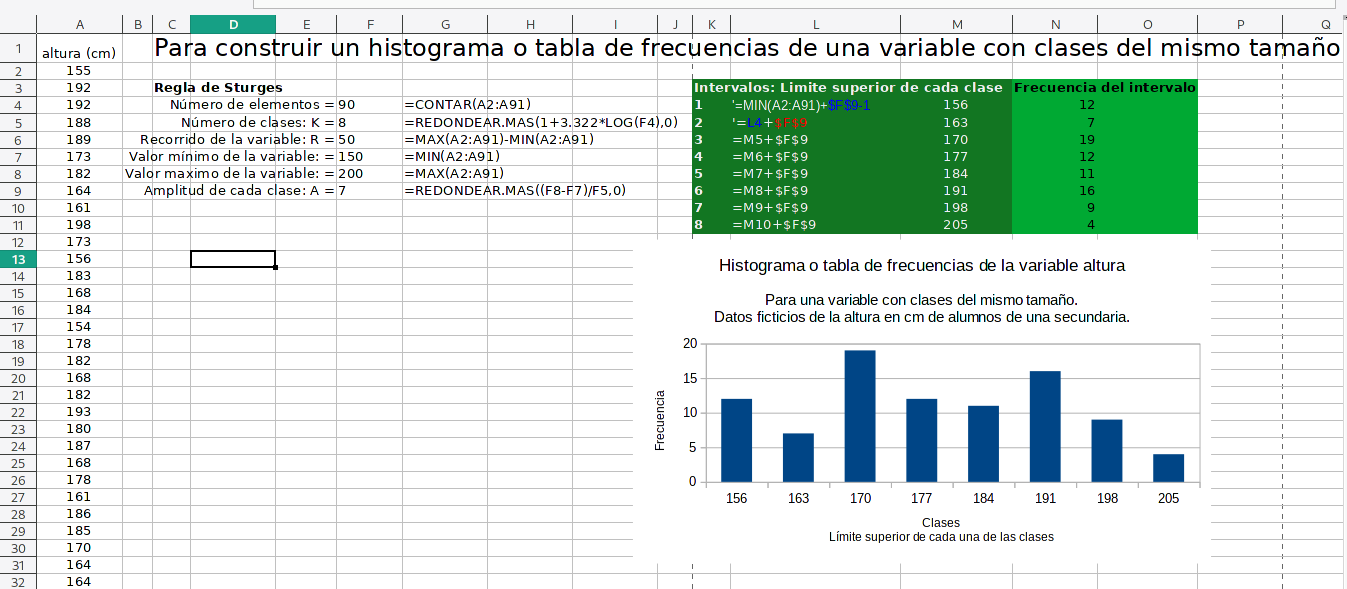
En una columna tengo cada uno de los valores de la variable altura. A partir de estos datos calculo el valor máximo y el mínimo encontrados en el recorrido (o intervalo) de la variable y cuento cuántos elementos o registros hay en la columna. Con estos resultados obtengo la amplitud y cantidad de clases necesarias para construir la tabla de frecuencias.

Para construir la tabla de frecuencias, anoto en una columna el límite superior de cada clase (para calcular esto uso la regla de Sturges) y, usando la fórmula matricial FRECUENCIA en una columna adyacente, calculo la frecuencia de cada clase.

Todo esto se verá más claro en el ejemplo que puedes descargar aquí mismo: histograma.ODS.

Para ejemplos más complejos, como un histograma de la densidad de frecuencia de una variable, mejor pregunta en ask.libreoffice.org.

Referencias

• Ayuda en línea de LibreOffice para la función FRECUENCIA: https://help.libreoffice.org/latest/es/text/scalc/01/04060107.html.
• Cómo calcular la amplitud y número de clases para una tabla de frecuencia de una variable de acuerdo a la regla de Sturges.

2. Resúmenes numéricos: medidas de dispersión, de centralidad y forma

Para obtener los valores resumen más importantes de un conjunto de datos (una variable), basta con seleccionar el intervalo donde están los datos, incluyendo las etiquetas de nombre de cada columna o fila (dependiendo cómo se presentan los datos). Después, vamos al menú Datos > Estadísticas > Estadísticas descriptivas… En el diálogo que aparece, confirmamos el intervalo de celdas donde están nuestros datos, definimos dónde escribirá Calc los resultados y cómo están organizados los datos de entrada, si por filas o columnas.

El resultado, para un ejercicio muy sencillo donde obtengo el resumen de 3 variables diferentes, Matemáticas, Física y Biología será algo como esto:

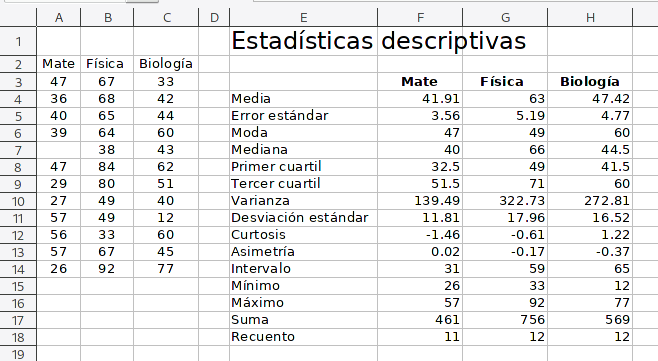
Puedes descargar el ejemplo con que elaboré la imagen de arriba: estadistica-descriptiva.ODS.

Por supuesto, es posible obtener los resultados de manera individual con las fórmulas de Calc: PROMEDIO, MEDIA, VAR (varianza), CONTAR, MODA, MEDIANA, CUARTIL, DESVEST (desviación estándar), CURTOSIS, COEFICIENTE.ASIMETRIA, MAX (valor máximo) y MIN (valor mínimo).

Medidas de centralidad

Las medias de centralidad, tendencia central o posición nos indican donde se sitúa un dato dentro de una distribución de datos. Las funciones que podemos ocupar son MEDIA, MEDIANA y MODA, ya mencionadas arriba.

Medidas de dispersión

Las medidas de dispersión, variabilidad o variación nos indican si los datos están próximos entre sí o dispersos; es decir, nos indican cuán esparcidos o distantes se encuentran en relación con un cierto valor central. También podremos identificar la concentración de los mismos en un cierto sector de la distribución y, por ende, podremos estimar cuán dispersas están dos o más distribuciones de datos. Estas medidas, entonces, nos permiten evaluar la confiabilidad del valor del dato central de un conjunto de datos, siendo la media aritmética el dato central más utilizado.

Cuando existe una dispersión pequeña se dice que los datos están dispersos o acumulados cercanamente respecto a un valor central; en este caso, el
dato central es un valor muy representativo. En el caso que la dispersión sea grande, el valor central no es muy confiable. Cuando una distribución de datos tiene poca dispersión toma el nombre de distribución homogénea y si su dispersión es alta se llama heterogénea.

• Ya en otra ocasión, nuestro querido amigo @Bozo (Ameck Bozo), nos mostró en un video cómo realizar medidas de dispersión y de regresión usando LibreOffice Calc. Compartimos aquí su presentación de Impress, la entrada en el blog de LibreOffice Hispano y su vídeo en YouTube.
• Aunque es un poco antiguo el Calc usado en esta versión, sigue siendo muy útil la charla de José Loureiro que publicó en su canal de YouTube.

Medidas de forma

Contamos con el coeficiente de asimetría y con el coeficiente de apuntamiento o curtosis para conocer la forma de la distribución de la variable en nuestros datos.

Dependiendo del valor del coeficiente de asimetría, la distribución de datos se agrupará o no hacia algún lado del eje X. Con la función COEFICIENTE.ASIMETRIA se revela hacia dónde se inclina o sesga la distribución de los datos.

• Si el coeficiente de asimetría es cero, la distribución es simétrica alrededor de la media.
• Si es coeficiente de asimetría es mayor a cero, la distribución es asimétrica hacia la derecha.
• Si es coeficiente de asimetría es menor a cero, la distribución es asimétrica hacia la izquierda.

La curtosis mide la mayor o menor cantidad de datos que se agrupan en torno a la moda. Usemos la función CURTOSIS para encontrar la forma de la distribución de los datos de nuestra variable. Se definen 3 tipos de distribuciones (3 tipos de forma de la distribución de los datos), según su grado de curtosis:

• Distribución mesocúrtica: presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal). La curtosis es igual a cero y la distribución es similar a la distribución normal de Gauss.
• Distribución leptocúrtica: presenta un elevado grado de concentración alrededor de los valores centrales de la variable. La curtosis es mayor a cero y la distribución es más puntiaguda.
• Distribución platicúrtica: presenta un reducido grado de concentración alrededor de los valores centrales de la variable. La curtosis es menor a cero y la distribución es más plana, pues los datos tienden hacia los extremos.

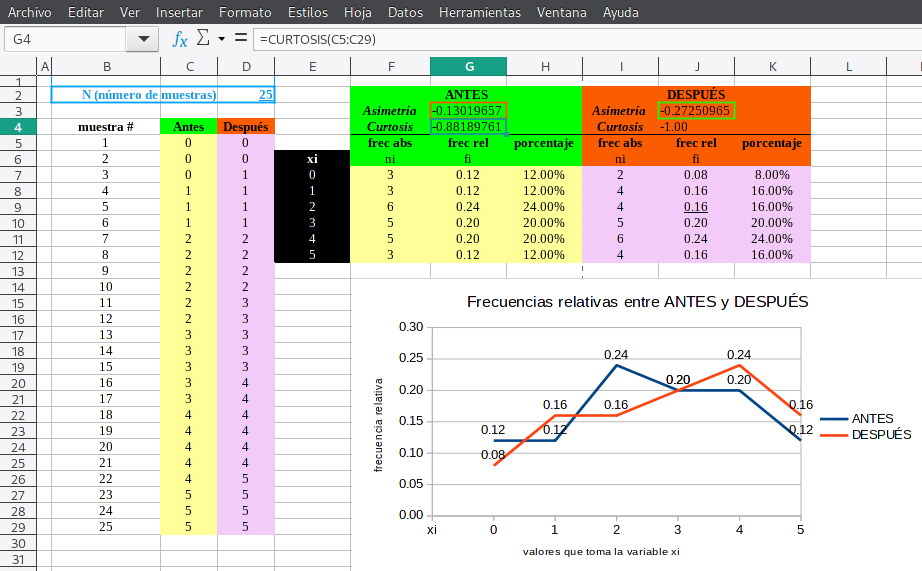
Ahora bien, consideremos el siguiente ejemplo, donde hemos construido dos histogramas para sendas variables. Hemos comparado las curvas de las frecuencias y determinado el coeficiente de asimetría y la curtosis de cada una. Podemos verlo todo en la siguiente ilustración (también está el archivo correspondiente). Usando el asistente de gráficos, elegí el de líneas y puntos para generar una visualización del histograma de cada variable. El archivo está aquí: asimetria-distribucion-normal.ods.

Los cálculos de centralidad se emplean, generalmente, para relacionar dos variables entre sí. En este caso, y por comodidad y facilidad de uso del asistente de gráficas de Calc, se recomienda poner la variable que utilizaremos en el eje X de la gráfica en la primera columna de la tabla donde guardaremos los datos que vamos a analizar.

Referencias

• Ejemplos de uso y cálculo de medidas de dispersión del GIEAO.
• ML2Projects. Machine Learning 2 Projects: blog divulgativo sobre ciencia de datos, aprendizaje de máquina y estadística.

3. Estadística descriptiva de dos o más variables: matriz de covarianza, coeficiente de correlación y regresión lineal simple

Para realizar análisis donde consideramos dos variables por cada observación, es muy común usar las herramientas mencionadas en este rubro.

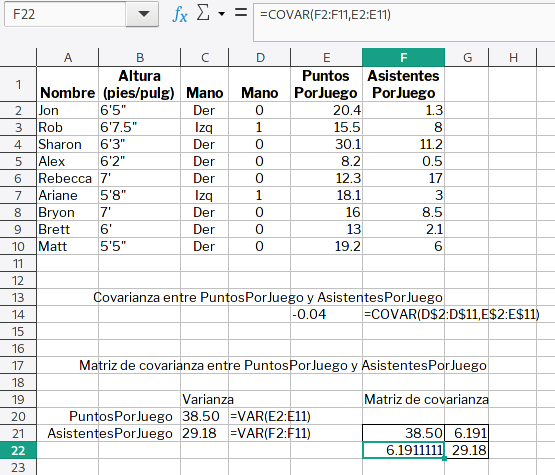
Dicen nuestros maestros de HojaMat.es: «La covarianza mide el paralelismo existente entre ambas variables (en función solo de los datos presentes en la tabla). Si la covarianza es grande, manifestará la existencia de un cierto paralelismo o dependencia (en sentido estadístico) entre X e Y. Si es pequeña, indicará que ambas variables se comportan de manera más independiente.» Podemos usar la función COVAR para determinar el paralelismo entre la mano que usa cada jugador de básquetbol y el promedio de puntos que anota por juego, como en el ejemplo de más abajo. Como siempre, aquí está el archivo: varianza-y-matriz-de-covarianza.ods.

El ejemplo es muy sencillo, solo para mostrar cómo hacer los cálculos. En el caso de la matriz de covarianza de dos variables, y ya que la matriz de covarianza siempre es simétrica y la covarianza entre dos variables no depende del orden de las variables, entonces la covarianza de (X,Y) es igual a la covarianza de (Y,X).

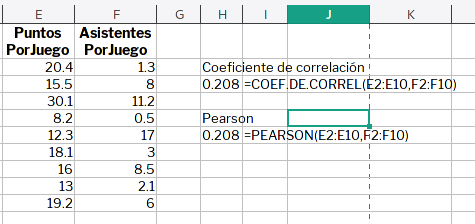
Como la covarianza no tiene un valor máximo, nos impide valorar el grado de paralelismo existente en los datos. Entonces se utiliza un método de normalización en el que se divide la covarianza entre la desviación para obtener el coeficiente de correlación entre los datos. El coeficiente de correlación, r, también se llama coeficiente de Pearson. Hay dos funciones de LibreOffice que se usan en este caso: COEF.DE.CORREL y PEARSON.

La regresión lineal simple nos permite hacer pronósticos para nuevos valores de alguna variable, especialmente si hay un grado de paralelismo significativo. Otra vez ponemos un ejemplo sencillo que solo ilustre cómo usar LibreOffice para obtener un modelo funcional. El archivo de trabajo es regresion-lineal.ods. Según la documentación que he revisado (confieso que no soy experta en estadística), hay dos maneras para obtener los coeficientes de la ecuación lineal que presumiblemente definirá la tendencia de nuestra variable Y, de acuerdo a los datos de la variable X. He usado las funciones COVAR,VARIANZA,PROMEDIO,PENDIENTE e INTERSECCION.EJE para realizar los cálculos en la hoja.

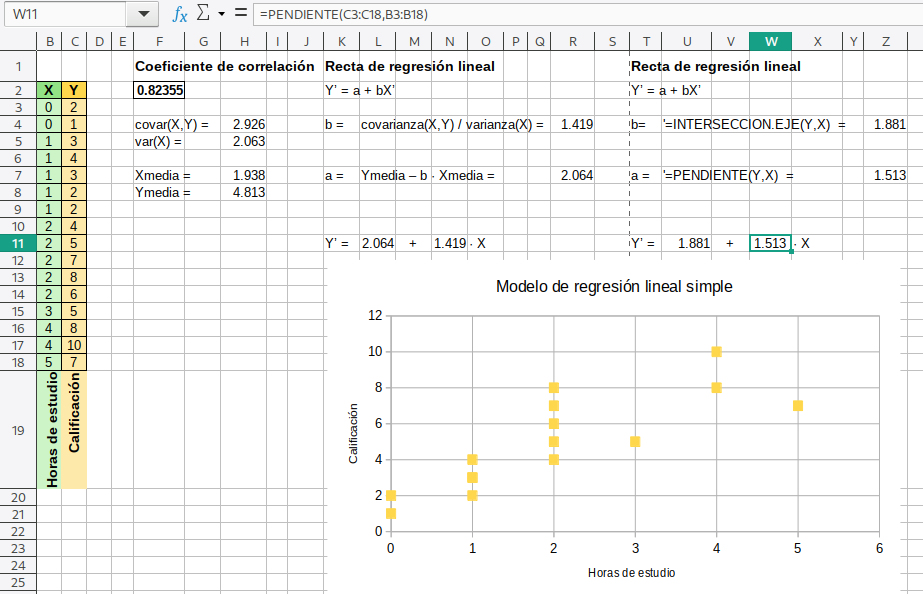
En el ejemplo del archivo hemos usado los dos métodos que encontré. Si alguien me corrige, estoy abierta a sus comentarios constructivos. La primera ilustración muestra los cálculos hasta construir el diagrama de dispersión XY.

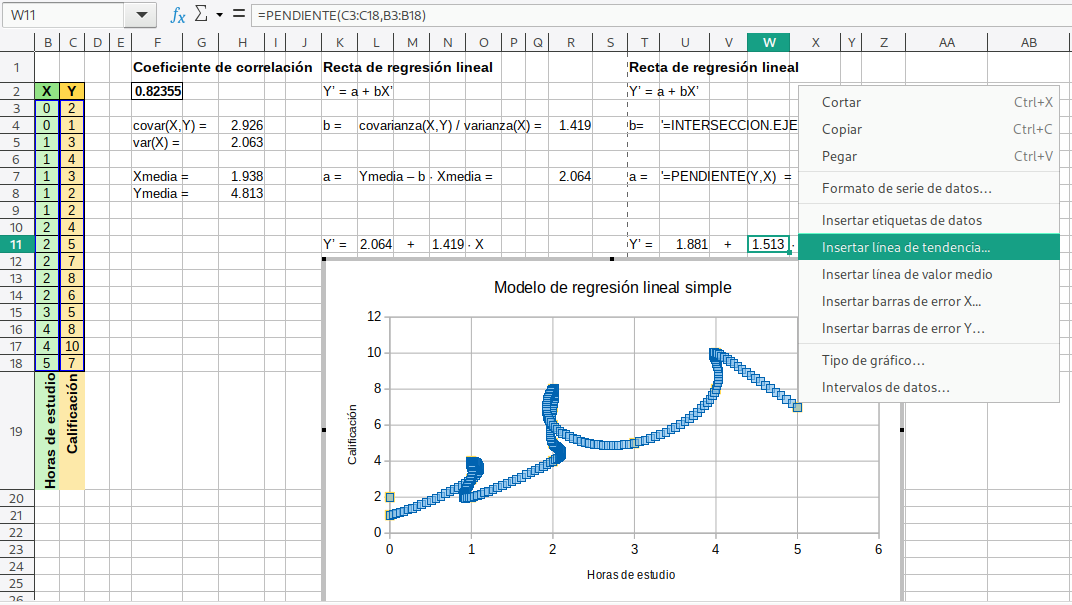
Después, haciendo doble clic en cualquiera de los puntos del diagrama aparecerá una curva de muchos más puntos, como se muestra en el paso 2. Ahí, mediante el menú contextual, insertamos la línea de tendencia que nos convenga según los datos y el coeficiente de correlación (como es cercano a 1 es una relación directa). En este ejemplo elegí el tipo de ecuación lineal.

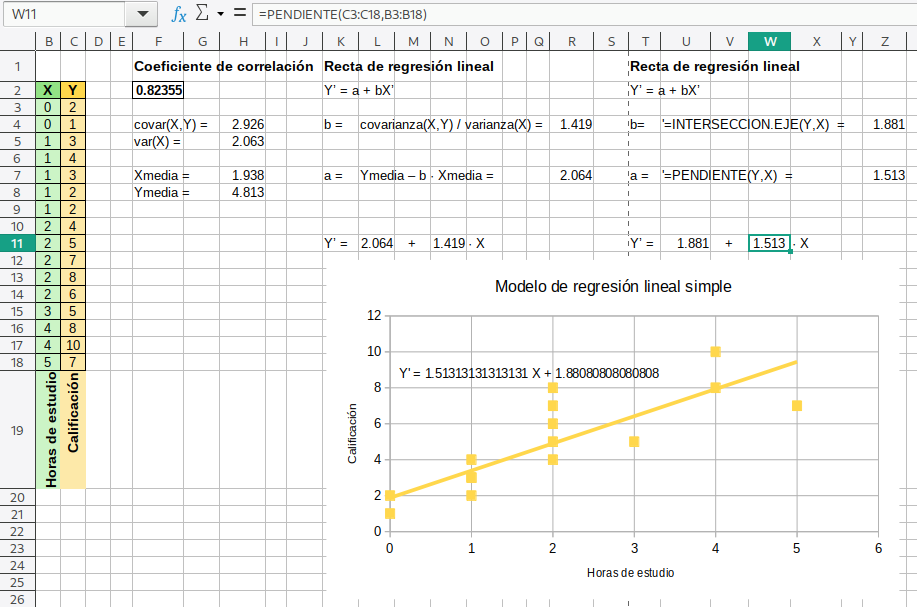
Finalmente, nuestro diagrama quedará así. Es posible cambiar el formato de cualquier elemento de la gráfica, incluso el de la línea de tendencia.

Referencias

• https://www.probabilidadyestadistica.net/matriz-de-covarianza/
• http://www.hojamat.es/estadistica/tema4/teoria/teoria4.pdf

---

Hay mucho que explorar aún, pero vamos poco a poco…